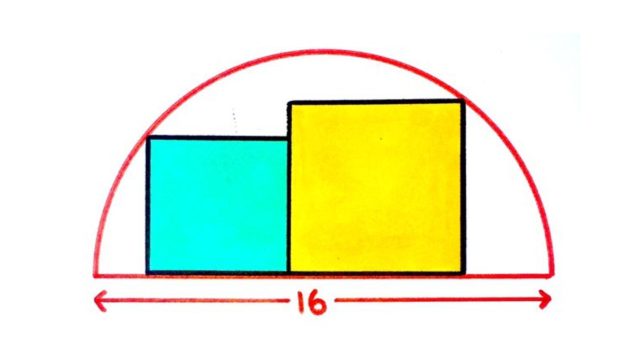
Twitterで拾った問題 半円に接する2つの正方形 オンライン講師ブログ
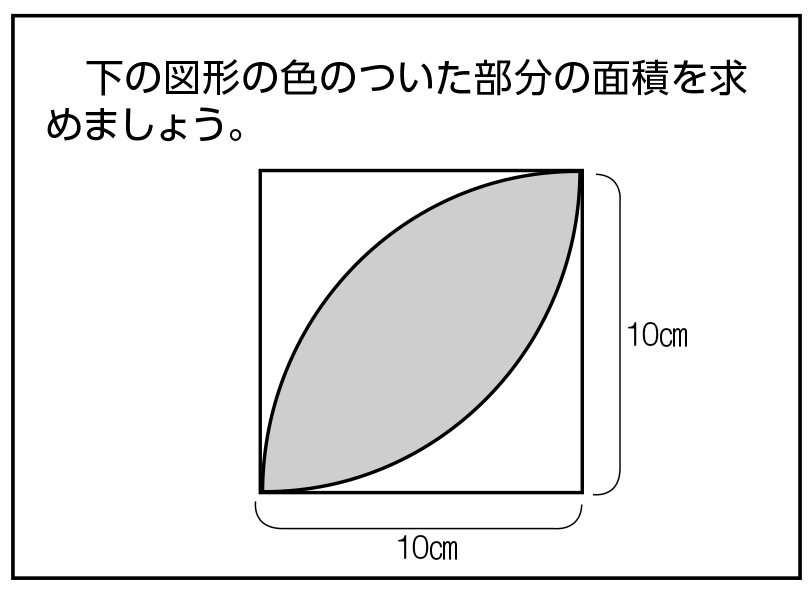
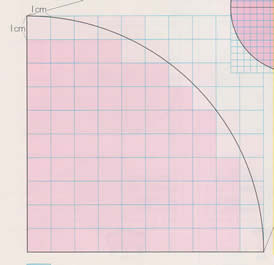
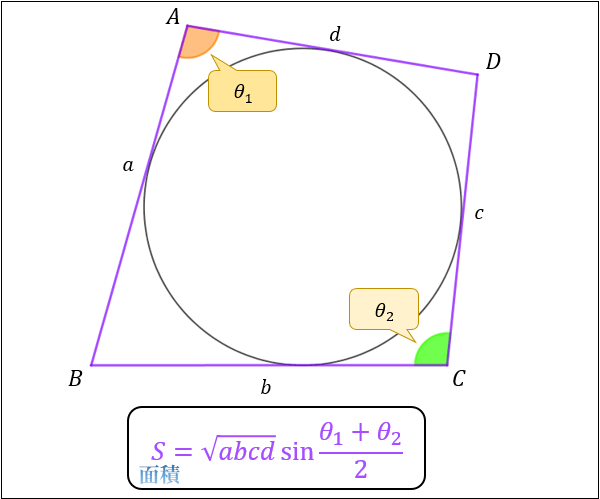
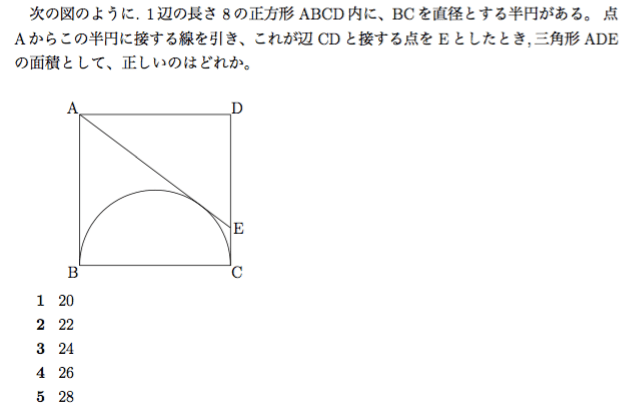
三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度 設問は図で示された斜線の部分の面積を求めなさいという 問題でしたので、図を文章にしてみました。 問題 一辺10cmの正方形abcdにおいて、 点aを中心として正方形abcdに内接する4分の1円を描く。 同様に、点bを中心として正方形abcdに内接する4分の1円を
円 内接 正方形 面積
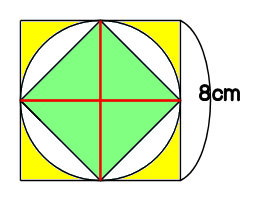
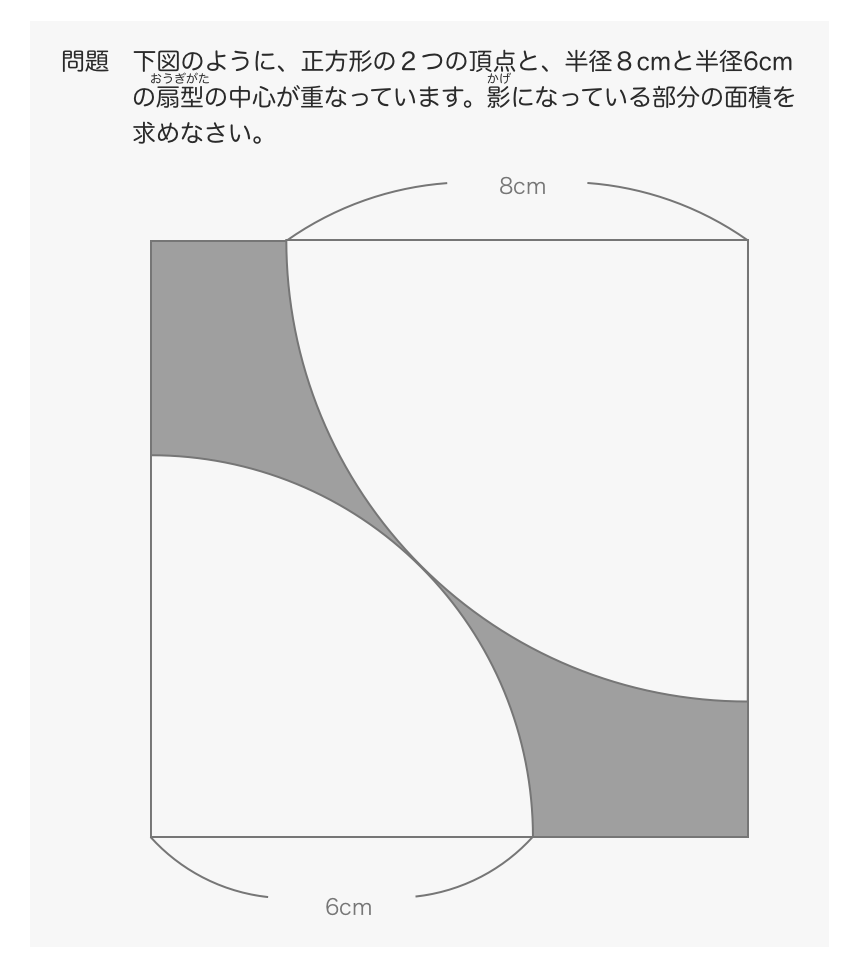
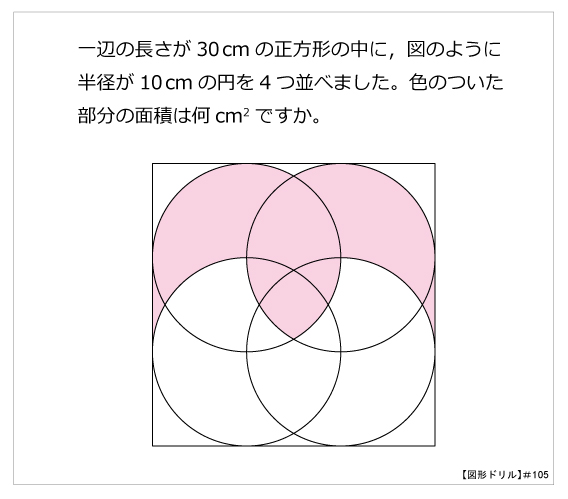
円 内接 正方形 面積-面積の計算 ・正三角形の面積 ・三角形の面積(底辺と高さ) ・三角形の面積(2辺と間の角度) ・三角形の面積(1辺と両端の角度) ・三角形の面積(3辺の長さ) ・正方形の面積 ・長方形の面積 ・台形の面積 ・ひし形の面積 ・平行四辺形の面積(底辺と高さ)円とおうぎ形⑹ 弓形の面積 16 16 次の図は、1辺8㎝の正方形ABCDと、直径8㎝の円を4個組み合 わせた図形です。色のついた部分の面積を求めなさい。ただし円周率 は314とします。
小6算数 円の面積 指導アイデア 2 みんなの教育技術
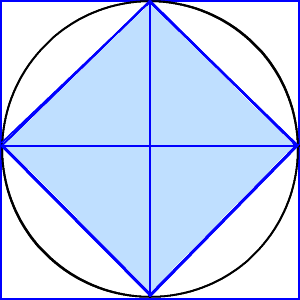
円の面積 円の面積は，半径×半径×314で求められます。 この求積公式の指導にあたっては，公式の理解はもとより，そこに至る過程を大切に指導することが重要です。 まず，半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるか円の面積にπ分の4を掛けたら、どうなるでしょうか。 π×π分の4 = 4と先ほどから言っていますので、 円の面積にπ分の4を掛けたら、円を囲む正方形の面積が出るはずです。 では試しに、円の半径を3cmとして計算してみましょう。小さな正方形になる、ピッタリ重なるから、半分の面積だ。 答え 32c㎡ 考え方2 中の正方形の4分の1の面積をもとめ、その4倍をすれば良い。 4分の1の三角形の、たてと横のながさは、4cm だから が小さな三角形で その4倍が正方形だから 扇形と正方形
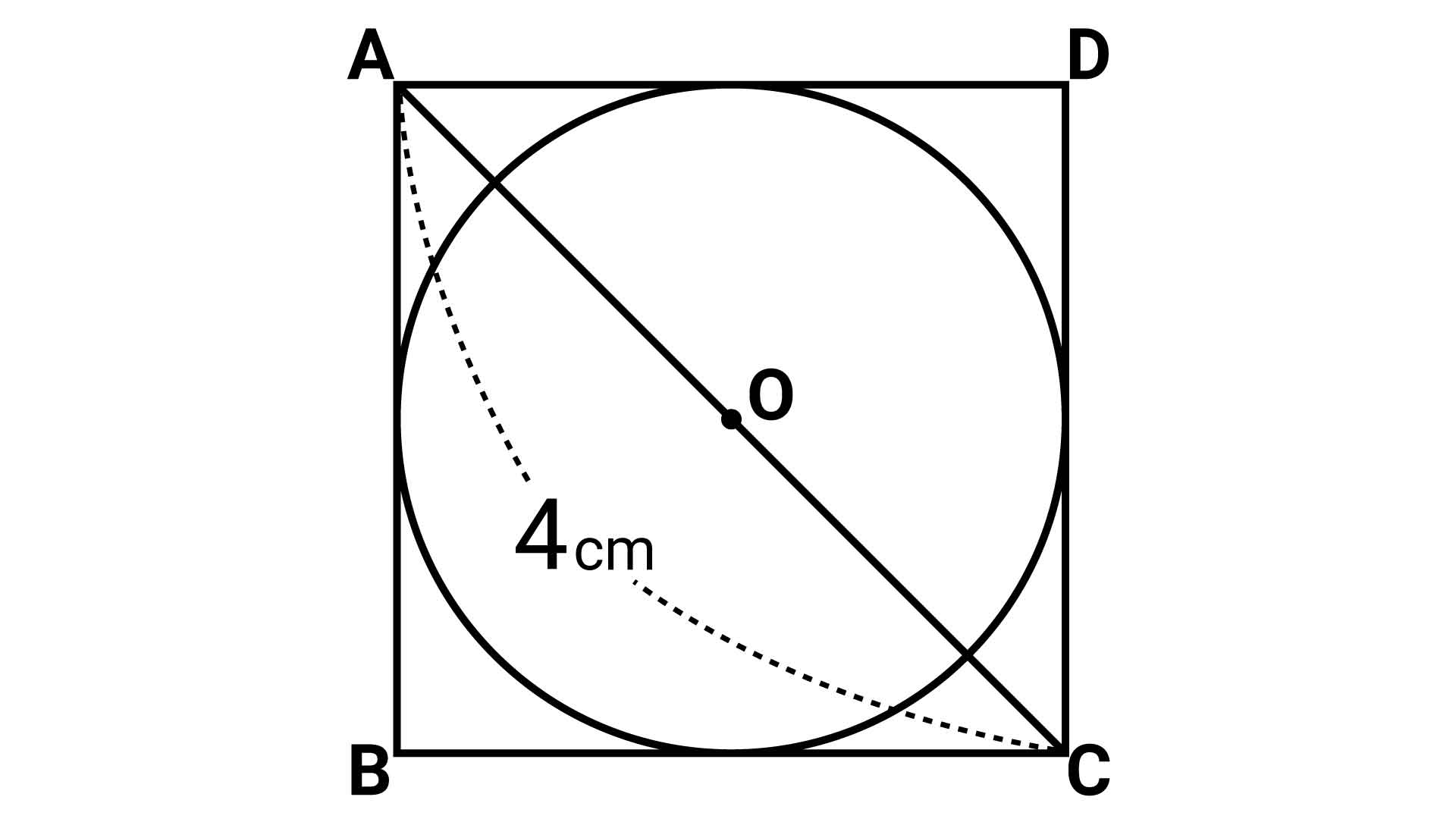
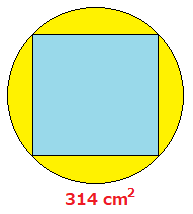
A=面積 a=面積 a=面積 もし とすれば a=面積 a=面積 もし とすれば a=面積 p=楕円の周囲 a=πab 、pを求める近似式 a=面積 a=面積bcd a=面積 なお点線に示すよう二つの三角形となし 各々の面積を計算しその和をもって 不平行四辺形の面積を算出してもよい =弧の色のついた部分の面積を求めなさい。ただし円 周率は314とします。 円とおうぎ形⑺ 正三角形が関係する問題 11 17 次の図1は正方形の中に正三角形を2個かいた図形で、図2は正方形正方形に接するように円があります。 正方形の一辺の長さは4センチメートルです。 この円の面積は何平方センチメートルでしょう。 円周率を3．14として面積を求めなさい。 この問題は案外応用問題がたくさんある。 クマ 半径が分からなきゃ面積は出
円 内接 正方形 面積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 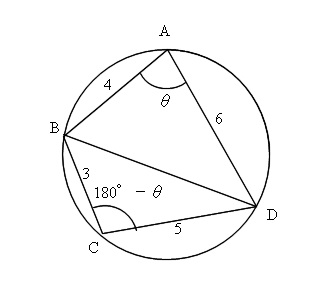 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 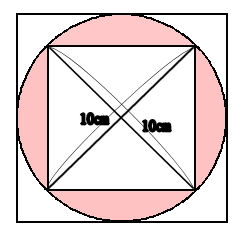 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 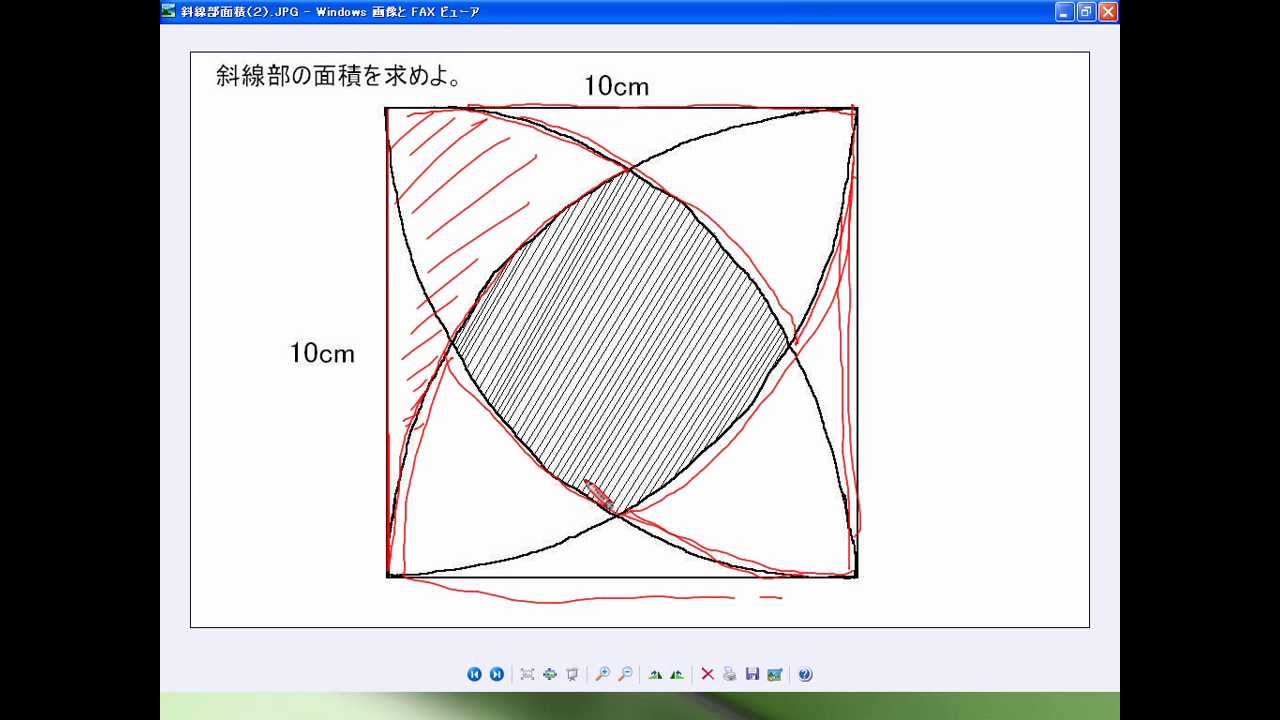 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 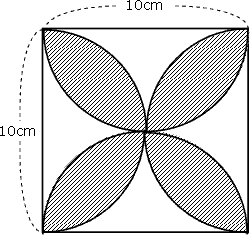 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 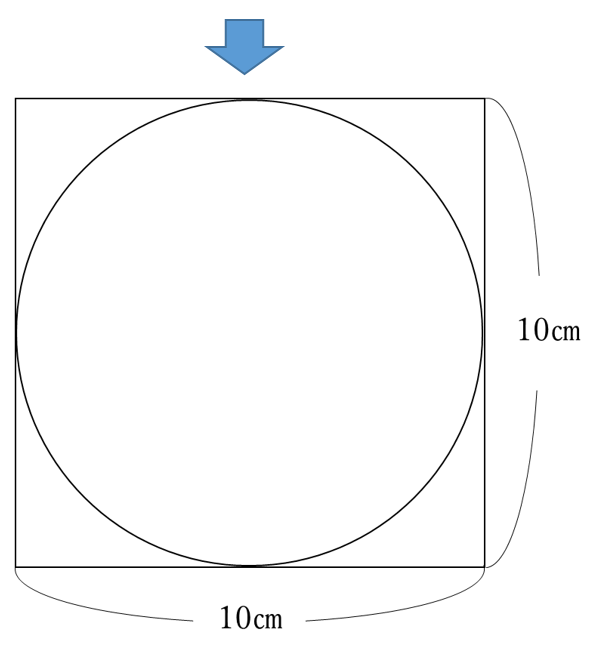 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 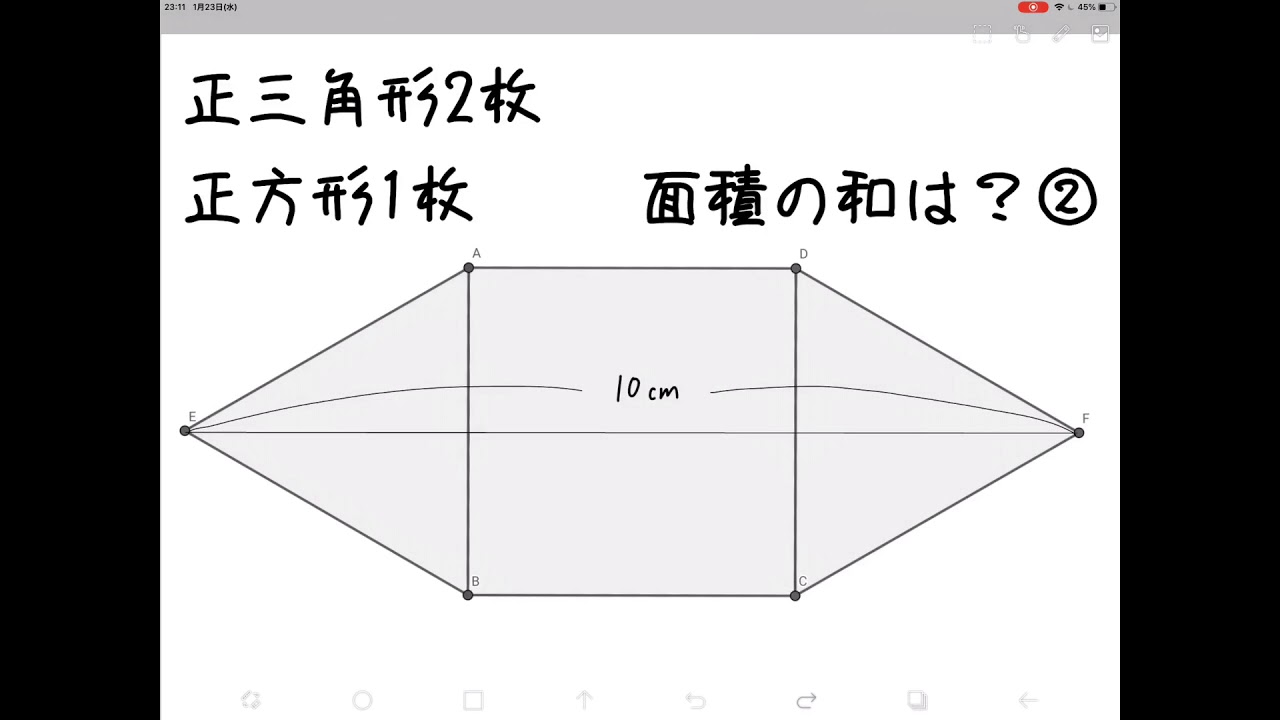 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 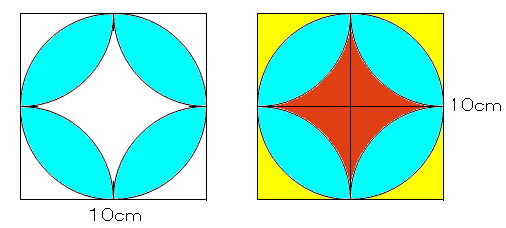 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 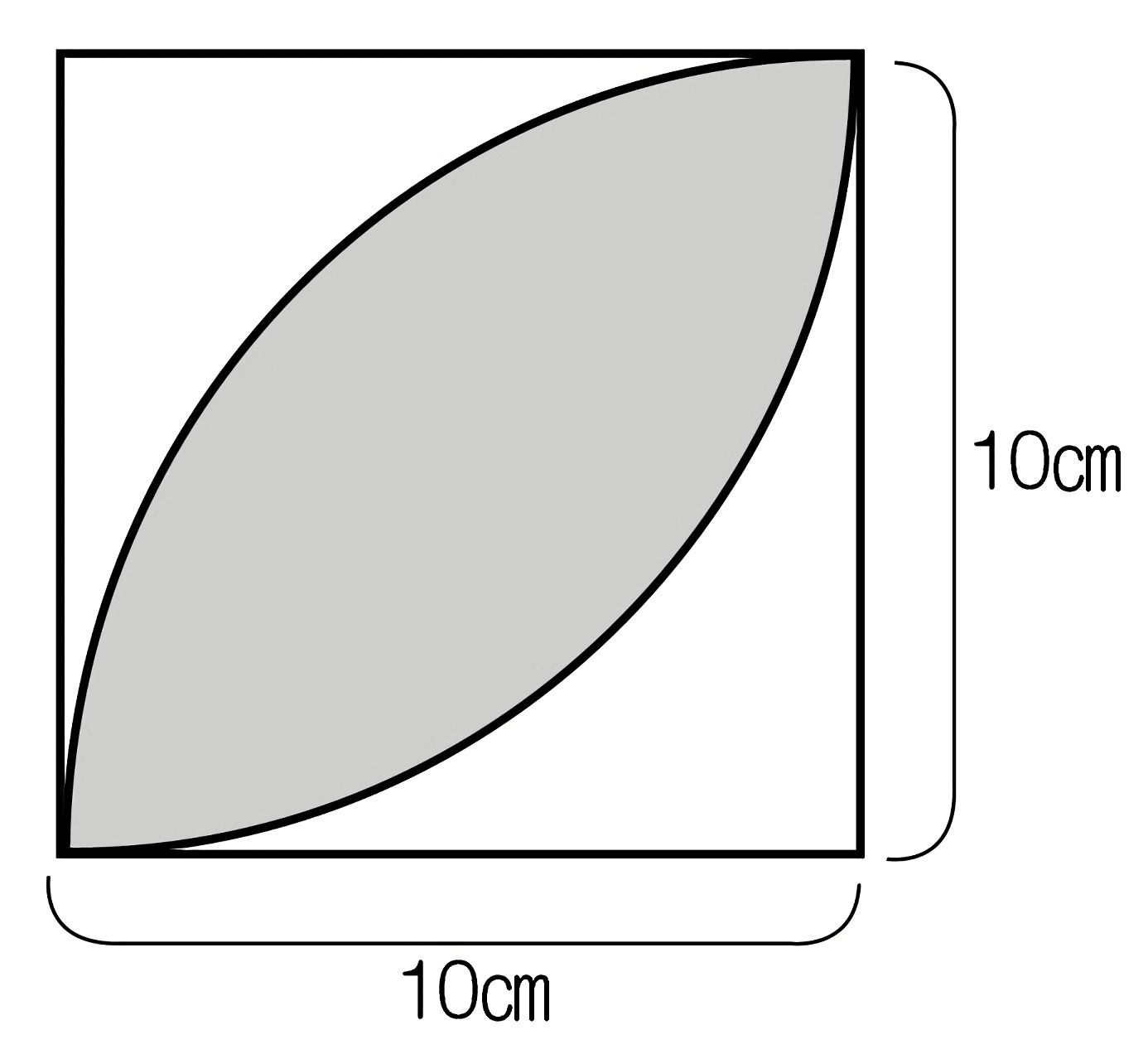 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト | 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |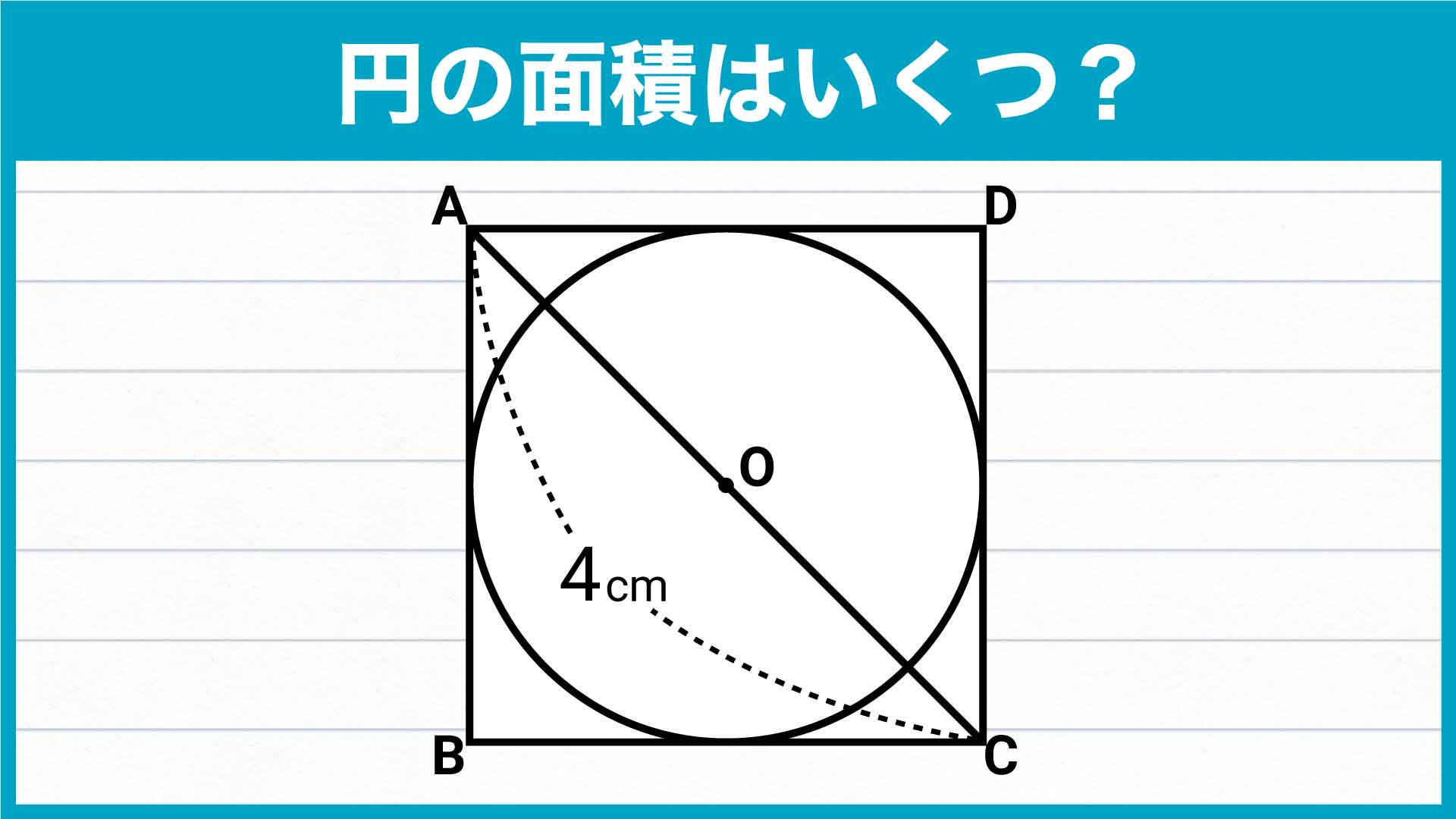
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
「円 内接 正方形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
 図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |  図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト |
正六角形の切断 s ü ⃝2 は，右の図から2になることがわかります。 ⃝3 は，正六角形の面積を6とすると，長方形は 6 1 2 = 4となります。 例題 面積が12cm2 の正六角形があります。 この六角形の頂点を結んで作った，図形⃝1 ，⃝2 の面積は，それぞれSAPIX (サピックス)4年 みんな知らない！ 「円の面積＝正方形×314」です サピックスでは、057の公式を4年生で習うんですね。 他塾と比較してかなり早いです。 いや、057の公式は教えてない塾の方が多い。 市販の問題集を見ても、057の公式を紹介して
Incoming Term: 円 正方形 面積, 円 正方形 面積 同じ, 円 正方形 面積比, 円 内接 正方形 面積, 数学 円 正方形 面積, 正方形 円 面積 中学受験, 正方形 円 重なる 面積, 正方形 円 面積 問題, 図形 面積 正方形 円,
0 件のコメント:
コメントを投稿